In this second part of our machine learning series, we’ll implement the same MNIST classification task using TensorFlow. While Scikit-learn excels at classical machine learning, TensorFlow shines when building neural networks. We’ll see how deep learning approaches differ from traditional methods and learn the basic concepts of neural network architecture.

The complete code for this tutorial can be found in the 02_tensorflow_simple.py script.

Why Neural Networks?

While our Scikit-learn models performed well in Part 1, neural networks offer several key advantages for image classification:

  • Automatic feature learning: No need to manually engineer features
  • Scalability: Can handle much larger datasets efficiently
  • Complex pattern recognition: Especially good at finding hierarchical patterns in data
  • State-of-the-art performance: Currently the best approach for many computer vision tasks

Let’s see these advantages in action by building our own neural network for digit classification.

Let’s start by importing the necessary packages:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

1. Load and Prepare Dataset

Unlike Scikit-learn, TensorFlow’s MNIST dataset comes in a slightly different format. We’ll keep the images in their original 2D shape (28x28 pixels) since neural networks can work directly with this structure - another advantage over traditional methods.

# Model parameters
num_classes = 10  # One class for each digit (0-9)
input_shape = (28, 28, 1)  # Height, width, and channels (1 for grayscale)

# Load dataset, already pre-split into train and test set
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()

# Scale pixel values to range [0,1] - this helps with training stability
x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0

# Add channel dimension required by Conv2D layers
# Shape changes from (samples, height, width) to (samples, height, width, channels)
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)

print("x_train shape:", x_train.shape)
print("x_test shape:", x_test.shape)

x_train shape: (60000, 28, 28, 1)
x_test shape: (10000, 28, 28, 1)

Our dataset dimensions represent:

  • 60,000 training samples: Much larger than scikit-learn’s version for better learning
  • 28x28 pixels: Higher resolution images than Part 1’s 8x8 grid
  • 1 channel: Grayscale images (RGB would be 3 channels)
  • 10,000 test samples: Large test set for robust evaluation

The final dimension (1) represents the color channel. Since MNIST contains grayscale images, we only need one channel, unlike RGB images which would have 3 channels.

Now that the data is loaded and scaled to appropriate range, we can go ahead and create the neural network model. Given that our input are images, let’s go ahead and train a convolutional neural network. There are multiple ways how we can set this up.

2. Create Neural Network Model

For image classification, we’ll use a Convolutional Neural Network (CNN). CNNs are specifically designed to work with image data through specialized layers:

  • Convolutional layers: Extract spatial features like edges, textures, and shapes
  • Pooling layers: Reduce spatial dimensions while preserving important features
  • Dense layers: Combine extracted features for final classification
  • Dropout layers: Prevent overfitting by randomly deactivating neurons during training

There are multiple ways to define a model in TensorFlow. Let’s explore two common approaches:

2.1. Sequential API

The Sequential API is the simplest way to build neural networks - layers are stacked linearly, one after another:

# Define model architecture using Sequential API
model = keras.Sequential(
    [
        # First Convolutional Block (32 filters, each 3x3 in size, detect basic patterns)
        layers.Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=input_shape),

        # MaxPooling2D: Reduces spatial dimensions by half while preserving features
        layers.MaxPooling2D(pool_size=(2, 2)),

        # Second Convolutional Block (64 filters, detect more complex patterns)
        layers.Conv2D(64, kernel_size=(3, 3), activation='relu'),

        # MaxPooling2D: Reduces spatial dimensions by half while preserving features
        layers.MaxPooling2D(pool_size=(2, 2)),

        # Flatten 3D feature maps to 1D feature vector
        layers.Flatten(),

        # Dense layers for final classification
        layers.Dropout(0.5),  # Prevents overfitting by randomly dropping 50% of connections
        layers.Dense(32, activation='relu'),  # Hidden layer combines features

        # Output layer for classification
        layers.Dense(num_classes, activation='softmax'),
    ]
)

2.2. Layer-by-Layer Sequential API

For more explicit control, we can separate each layer and activation:

# More precise and sequential approach
model = keras.Sequential(
    [
        keras.Input(shape=input_shape),
        layers.Conv2D(32, kernel_size=(3, 3)),
        layers.ReLU(),
        layers.MaxPooling2D(pool_size=(2, 2)),
        layers.Conv2D(64, kernel_size=(3, 3)),
        layers.ReLU(),
        layers.MaxPooling2D(pool_size=(2, 2)),
        layers.Flatten(),
        layers.Dropout(0.5),
        layers.Dense(32),
        layers.ReLU(),
        layers.Dropout(0.5),
        layers.Dense(num_classes),
        layers.Softmax(),
    ]
)

The two models are functionally identical, but the layer-by-layer approach offers several advantages:

  • Makes it easier to insert additional layers like BatchNormalization
  • Provides more explicit activation functions
  • Makes the data flow more transparent
  • Allows finer control over layer parameters

Next to this sequential API, there’s also a functional API.We’ll explore this more flexible approach in our advanced TensorFlow tutorial, which allows for:

  • Multiple inputs and outputs
  • Layer sharing
  • Non-sequential layer connections
  • Complex architectures like residual networks

Once the model is created, you can use the summary() method to get an overview of the network’s architecture and the number of trainable and non-trainable parameters.

model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                    Output Shape              Param #
=================================================================
conv2d (Conv2D)                 (None, 26, 26, 32)        320
re_lu (ReLU)                    (None, 26, 26, 32)        0
max_pooling2d (MaxPooling2D)    (None, 13, 13, 32)        0
conv2d_1 (Conv2D)               (None, 11, 11, 64)        18496
re_lu_1 (ReLU)                  (None, 11, 11, 64)        0
max_pooling2d_1 (MaxPooling2D)  (None, 5, 5, 64)          0
flatten (Flatten)               (None, 1600)              0
dropout (Dropout)               (None, 1600)              0
dense (Dense)                   (None, 32)                51232
re_lu_2 (ReLU)                  (None, 32)                0
dropout_1 (Dropout)             (None, 32)                0
dense_1 (Dense)                 (None, 10)                330
softmax (Softmax)               (None, 10)                0
=================================================================
Total params: 70,378 (274.91 KB)
Trainable params: 70,378 (274.91 KB)
Non-trainable params: 0 (0.00 Byte)
_________________________________________________________________

This summary tells us several important things:

  1. Our model has 70,378 trainable parameters - relatively small by modern standards
  2. The input image (28x28x1) is progressively reduced in size through pooling (see the Output Shape column)
  3. The final dense layer has 10 outputs - one for each digit class
  4. Most parameters are in the dense layers, not the convolutional layers

3. Train TensorFlow model

Before we can train the model we need to provide a few additional information:

  • batch_size: How many samples the model should look at once before performing the gradient descent.
  • epochs: For how many times the model should go through the full dataset.
  • loss: Which loss function the model should optimize for.
  • metrics: Which performance metrics the model should keep track of. By default this includes the loss metric.
  • optimizer: Which optimizer strategy the model should use. This could involve additional optimzation parameters, such as the learning rate.
  • validation_split or validation_data: This parameter allows you to automatically split the training set into a training and validation set (with validation_split) or you can also provide a specific validation set with validation_data.

Finding the right parameters for any of that, as well as establishing the right model architecture, is the black arts of any deep learning practitioners. For this example, let’s just go with some proven default parameters.

# Training configuration
batch_size = 128  # Number of samples processed before model update
epochs = 10       # Number of complete passes through the dataset

# Compile model with appropriate loss function and optimizer
model.compile(
    loss='sparse_categorical_crossentropy',  # Appropriate for integer labels
    optimizer='adam',                        # Adaptive learning rate optimizer
    metrics=['accuracy']                     # Track accuracy during training
)

# Train the model
history = model.fit(
    x_train,
    y_train,
    batch_size=batch_size,
    epochs=epochs,
    validation_split=0.1  # Use 10% of training data for validation
)

Epoch 1/10
422/422 [==============================] - 4s 9ms/step - loss: 0.5902 - accuracy: 0.8117 - val_loss: 0.1014 - val_accuracy: 0.9700
Epoch 2/10
422/422 [==============================] - 4s 8ms/step - loss: 0.2183 - accuracy: 0.9364 - val_loss: 0.0674 - val_accuracy: 0.9808
Epoch 3/10
422/422 [==============================] - 4s 8ms/step - loss: 0.1663 - accuracy: 0.9512 - val_loss: 0.0499 - val_accuracy: 0.9860
Epoch 4/10
422/422 [==============================] - 4s 8ms/step - loss: 0.1390 - accuracy: 0.9599 - val_loss: 0.0462 - val_accuracy: 0.9875
Epoch 5/10
422/422 [==============================] - 4s 8ms/step - loss: 0.1166 - accuracy: 0.9674 - val_loss: 0.0433 - val_accuracy: 0.9888
Epoch 6/10
422/422 [==============================] - 4s 8ms/step - loss: 0.1046 - accuracy: 0.9693 - val_loss: 0.0370 - val_accuracy: 0.9902
Epoch 7/10
422/422 [==============================] - 4s 8ms/step - loss: 0.0950 - accuracy: 0.9722 - val_loss: 0.0394 - val_accuracy: 0.9892
Epoch 8/10
422/422 [==============================] - 4s 8ms/step - loss: 0.0891 - accuracy: 0.9742 - val_loss: 0.0400 - val_accuracy: 0.9895
Epoch 9/10
422/422 [==============================] - 4s 8ms/step - loss: 0.0865 - accuracy: 0.9750 - val_loss: 0.0342 - val_accuracy: 0.9907
Epoch 10/10
422/422 [==============================] - 4s 8ms/step - loss: 0.0775 - accuracy: 0.9773 - val_loss: 0.0355 - val_accuracy: 0.9905

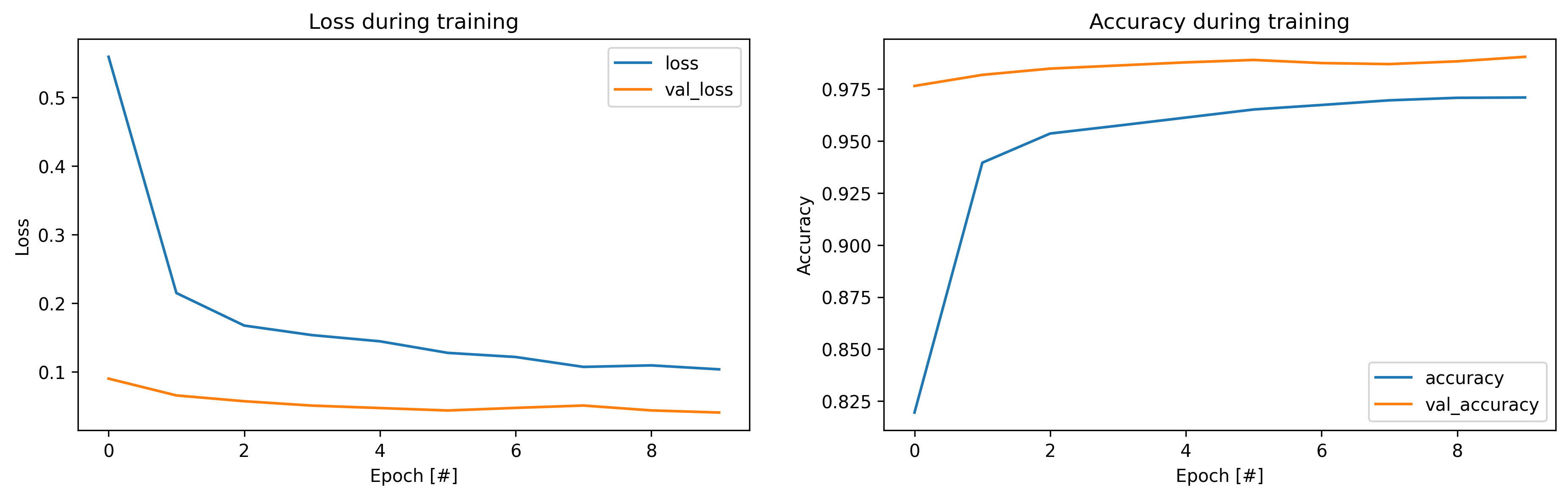
Let’s analyze the training progression:

  • Initial Performance (Epoch 1):
    • Training: 81.17% accuracy, loss of 0.5902
    • Validation: 97.00% accuracy, loss of 0.1014
    • Shows rapid initial learning
  • Final Performance (Epoch 10):
    • Training: 97.73% accuracy, loss of 0.0775
    • Validation: 99.05% accuracy, loss of 0.0355
    • Excellent convergence with validation outperforming training
  • Key Observations:
    • Consistent improvement across epochs
    • Lower validation loss than training loss suggests good generalization
    • Final accuracy exceeds our Scikit-learn model from Part 1
    • No signs of overfitting as validation metrics remain stable

4. Model investigation

If we stored the model.fit() output in a history variable, we can easily access and visualize the different model metrics during training.

# Store history in a dataframe
df_history = pd.DataFrame(history.history)

# Visualize training history
fig, axs = plt.subplots(1, 2, figsize=(15, 4))
df_history.iloc[:, df_history.columns.str.contains('loss')].plot(
    title="Loss during training", ax=axs[0])
df_history.iloc[:, df_history.columns.str.contains('accuracy')].plot(
    title="Accuracy during training", ax=axs[1])
axs[0].set_xlabel("Epoch [#]")
axs[1].set_xlabel("Epoch [#]")
axs[0].set_ylabel("Loss")
axs[1].set_ylabel("Accuracy")
plt.show()

Figure 1: Training metrics over time showing model loss (left) and Mean Absolute Error (right) for both training and validation sets. The logarithmic scale helps visualize improvement across different magnitudes.

Once the model is trained we can also compute its score on the test set. For this we can use the evaluate() method.

score = model.evaluate(x_test, y_test, verbose=0)
print(f"Test loss:     {score[0]:.3f}")
print(f"Test accuracy: {score[1]*100:.2f}%")

Test loss:     0.032
Test accuracy: 98.93%

And if you’re interested in the individual predictions, you can use the predict() method.

y_pred = model.predict(x_test, verbose=0)
y_pred.shape

(10000, 10)

Given that our last layer uses a softmax activation, we actually don’t get just the class label back, but the probability score for each class. To get to the class prediction, we therefore need to apply an argmax routine.

# Transform class probabilities to prediction labels
predictions = np.argmax(y_pred, 1)

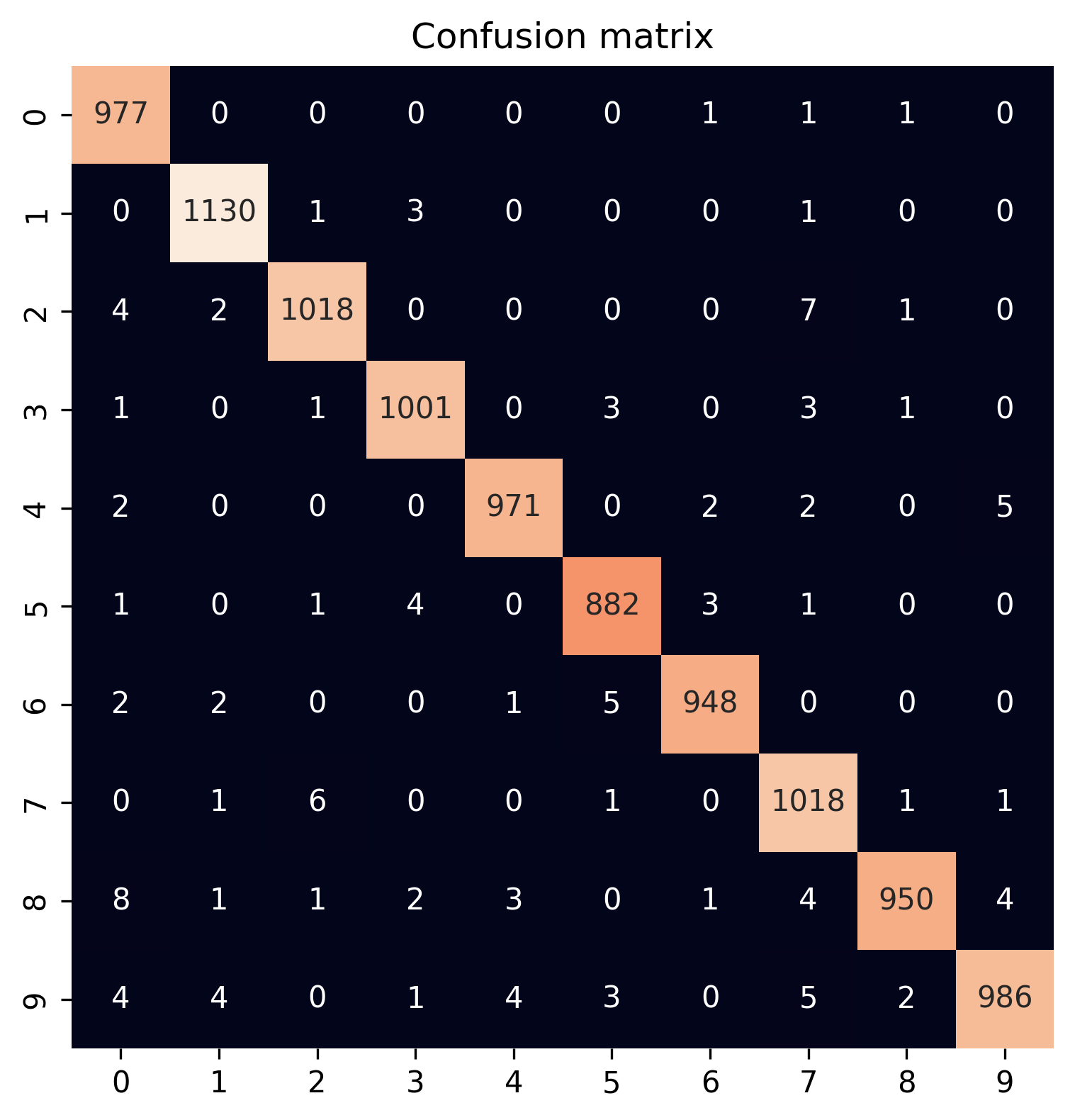
# Create confusion matrix
cm = tf.math.confusion_matrix(y_test, predictions)

# Visualize confusion matrix
plt.figure(figsize=(6, 6))
sns.heatmap(cm, square=True, annot=True, fmt='d', cbar=False)
plt.title("Confusion matrix")
plt.show()
Figure 2: Confusion matrix showing model predictions across all digit classes. The strong diagonal pattern indicates high accuracy across all digits.

5. Model parameters

And if you’re interested in the model parameters of the trained neural network, you can directly access them via model.layers. One advantage of neural networks is their ability to learn hierarchical features. Let’s examine what our first convolutional layer learned:

# Extract first hidden convolutional layers
conv_layer = model.layers[0]

# Transform the layer weights to a numpy array
weights = conv_layer.weights[0].numpy()

# Visualize the 32 kernels from the first convolutional layer
fig, axs = plt.subplots(4, 8, figsize=(10, 5))
axs = np.ravel(axs)

for idx, ax in enumerate(axs):
    ax.set_title(f"Kernel {idx}")
    ax.imshow(weights[..., idx], cmap='binary')
    ax.axis('off')
plt.tight_layout()
plt.show()

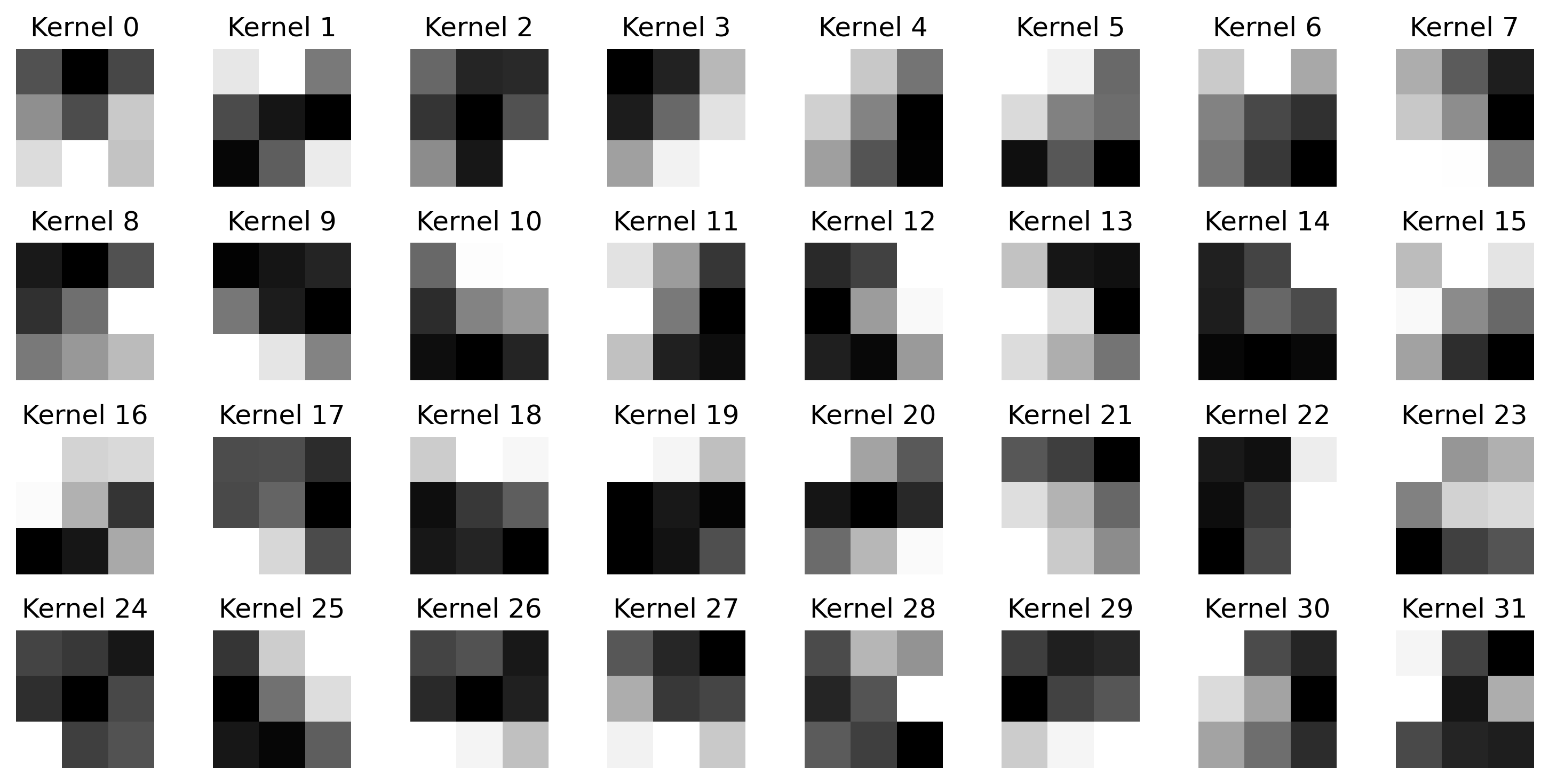
Figure 3: Visualization of the 32 convolutional kernels learned by the first layer. Each 3x3 kernel acts as a feature detector, learning to identify basic patterns like edges, corners, and textures that are useful for digit recognition.

Common Deep Learning Pitfalls

When starting with TensorFlow and neural networks, watch out for these common issues:

Data Preparation

  • (Almost) always scale input data (like we did with /255.0)
  • Check for missing or invalid values
  • Ensure consistent data types
# Example of proper data preparation
x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0

Model Architecture

  • Start simple, add complexity only if needed
  • Match output layer to your task (softmax for classification)
  • Use appropriate layer sizes
# Example of clear, progressive architecture
model = keras.Sequential([
    layers.Conv2D(32, kernel_size=(3, 3), activation='relu'),
    layers.MaxPooling2D(pool_size=(2, 2)),
    layers.Flatten(),
    layers.Dense(10, activation='softmax')  # 10 classes
])

Training Issues

  • Monitor training metrics (loss not decreasing)
  • Watch for overfitting (validation loss increasing)
  • Use appropriate batch sizes
# Add validation monitoring during training
history = model.fit(
    x_train, y_train,
    validation_split=0.1,
    batch_size=128,
    epochs=10
)

Memory Management

  • Clear unnecessary variables
  • Use appropriate data types
  • Watch batch sizes on limited hardware
# Free memory after training
import gc
gc.collect()
keras.backend.clear_session()

Summary and Next Steps

In this tutorial, we’ve introduced neural networks using TensorFlow:

  • Building a CNN architecture
  • Training with backpropagation
  • Monitoring learning progress
  • Visualizing learned features

Our neural network achieved comparable accuracy to our Scikit-learn models (~99%), but this time on images with a higher resolution with the potential for even better performance through further optimization.

Key takeaways:

  1. Neural networks can work directly with structured data like images
  2. Architecture design is crucial for good performance
  3. Training requires careful parameter selection
  4. Monitoring training helps detect problems early
  5. Visualizing learned features provides insights into model behavior

In Part 3, we’ll explore more advanced machine learning concepts using Scikit-learn, focusing on regression problems and complex preprocessing pipelines.

← Previous: Getting Started or Next: Advanced Machine Learning →