MapNode¶
If you want to iterate over a list of inputs, but need to feed all iterated outputs afterward as one input (an array) to the next node, you need to use a MapNode. A MapNode is quite similar to a normal Node, but it can take a list of inputs and operate over each input separately, ultimately returning a list of outputs.
Imagine that you have a list of items (let's say files) and you want to execute the same node on them (for example some smoothing or masking). Some nodes accept multiple files and do exactly the same thing on them, but some don't (they expect only one file). MapNode can solve this problem. Imagine you have the following workflow:
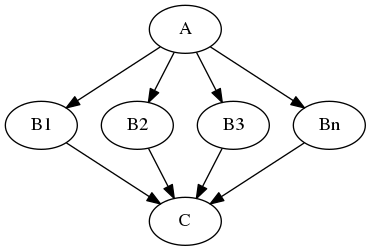
Node A outputs a list of files, but node B accepts only one file. Additionally, C expects a list of files. What you would like is to run B for every file in the output of A and collect the results as a list and feed it to C. Something like this:
from nipype import Node, MapNode, Workflow
a = Node(interface=A(), name="a")
b = MapNode(interface=B(), name="b", iterfield=['in_file'])
c = Node(interface=C(), name="c")
my_workflow = Workflow(name="my_workflow")
my_workflow.connect([(a,b,[('out_files','in_file')]),
(b,c,[('out_file','in_files')])
])
Let's demonstrate this with a simple function interface:
from nipype import Function
def square_func(x):
return x ** 2
square = Function(["x"], ["f_x"], square_func)
We see that this function just takes a numeric input and returns its squared value.
square.run(x=2).outputs.f_x
What if we wanted to square a list of numbers? We could set an iterable and just split up the workflow in multiple sub-workflows. But say we were making a simple workflow that squared a list of numbers and then summed them. The sum node would expect a list, but using an iterable would make a bunch of sum nodes, and each would get one number from the list. The solution here is to use a MapNode.
iterfield¶
The MapNode constructor has a field called iterfield, which tells it what inputs should be expecting a list.
from nipype import MapNode
square_node = MapNode(square, name="square", iterfield=["x"])
square_node.inputs.x = [0, 1, 2, 3]
res = square_node.run()
res.outputs.f_x
Because iterfield can take a list of names, you can operate over multiple sets of data, as long as they're the same length. The values in each list will be paired; it does not compute a combinatoric product of the lists.
def power_func(x, y):
return x ** y
power = Function(["x", "y"], ["f_xy"], power_func)
power_node = MapNode(power, name="power", iterfield=["x", "y"])
power_node.inputs.x = [0, 1, 2, 3]
power_node.inputs.y = [0, 1, 2, 3]
res = power_node.run()
print(res.outputs.f_xy)
But not every input needs to be an iterfield.
power_node = MapNode(power, name="power", iterfield=["x"])
power_node.inputs.x = [0, 1, 2, 3]
power_node.inputs.y = 3
res = power_node.run()
print(res.outputs.f_xy)
As in the case of iterables, each underlying MapNode execution can happen in parallel. Hopefully, you see how these tools allow you to write flexible, reusable workflows that will help you process large amounts of data efficiently and reproducibly.
In more advanced applications it is useful to be able to iterate over items of nested lists (for example [[1,2],[3,4]]). MapNode allows you to do this with the "nested=True" parameter. Outputs will preserve the same nested structure as the inputs.
Why is this important?¶
Let's consider we have multiple functional images (A) and each of them should be motioned corrected (B1, B2, B3,..). But afterward, we want to put them all together into a GLM, i.e. the input for the GLM should be an array of [B1, B2, B3, ...]. Iterables can't do that. They would split up the pipeline. Therefore, we need MapNodes.

Let's look at a simple example, where we want to motion correct two functional images. For this we need two nodes:
- Gunzip, to unzip the files (plural)
- Realign, to do the motion correction
from nipype.algorithms.misc import Gunzip
from nipype.interfaces.spm import Realign
from nipype import Node, MapNode, Workflow
# Here we specify a list of files (for this tutorial, we just add the same file twice)
files = ['/data/ds000114/sub-01/ses-test/func/sub-01_ses-test_task-fingerfootlips_bold.nii.gz',
'/data/ds000114/sub-01/ses-test/func/sub-01_ses-test_task-fingerfootlips_bold.nii.gz']
realign = Node(Realign(register_to_mean=True),
name='motion_correction')
If we try to specify the input for the Gunzip node with a simple Node, we get the following error:
gunzip = Node(Gunzip(), name='gunzip',)
try:
gunzip.inputs.in_file = files
except(Exception) as err:
if "TraitError" in str(err.__class__):
print("TraitError:", err)
else:
raise
else:
raise
TraitError: The 'in_file' trait of a GunzipInputSpec instance must be an existing file name, but a value of ['/data/ds000114/sub-01/ses-test/func/sub-01_ses-test_task-fingerfootlips_bold.nii.gz', '/data/ds000114/sub-01/ses-test/func/sub-01_ses-test_task-fingerfootlips_bold.nii.gz'] <class 'list'> was specified.
But if we do it with a MapNode, it works:
gunzip = MapNode(Gunzip(), name='gunzip',
iterfield=['in_file'])
gunzip.inputs.in_file = files
Now, we just have to create a workflow, connect the nodes and we can run it:
mcflow = Workflow(name='realign_with_spm')
mcflow.connect(gunzip, 'out_file', realign, 'in_files')
mcflow.base_dir = '/output'
mcflow.run('MultiProc', plugin_args={'n_procs': 4})
Exercise 1¶
Create a workflow to calculate a sum of factorials of numbers from a range between $n_{min}$ and $n_{max}$, i.e.:
$$\sum _{k=n_{min}}^{n_{max}} k! = 0! + 1! +2! + 3! + \cdots$$
if $n_{min}=0$ and $n_{max}=3$ $$\sum _{k=0}^{3} k! = 0! + 1! +2! + 3! = 1 + 1 + 2 + 6 = 10$$
Use Node for a function that creates a list of integers and a function that sums everything at the end. Use MapNode to calculate factorials.
#write your solution here
from nipype import Workflow, Node, MapNode, Function
import os
def range_fun(n_min, n_max):
return list(range(n_min, n_max+1))
def factorial(n):
# print("FACTORIAL, {}".format(n))
import math
return math.factorial(n)
def summing(terms):
return sum(terms)
wf_ex1 = Workflow('ex1')
wf_ex1.base_dir = os.getcwd()
range_nd = Node(Function(input_names=['n_min', 'n_max'],
output_names=['range_list'],
function=range_fun),
name='range_list')
factorial_nd = MapNode(Function(input_names=['n'],
output_names=['fact_out'],
function=factorial),
iterfield=['n'],
name='factorial')
summing_nd = Node(Function(input_names=['terms'],
output_names=['sum_out'],
function=summing),
name='summing')
range_nd.inputs.n_min = 0
range_nd.inputs.n_max = 3
wf_ex1.add_nodes([range_nd])
wf_ex1.connect(range_nd, 'range_list', factorial_nd, 'n')
wf_ex1.connect(factorial_nd, 'fact_out', summing_nd, "terms")
eg = wf_ex1.run()
let's print all nodes:
eg.nodes()
the final result should be 10:
list(eg.nodes())[2].result.outputs
we can also check the results of two other nodes:
print(list(eg.nodes())[0].result.outputs)
print(list(eg.nodes())[1].result.outputs)